Accelerate Python with Numba’s @jit(nopython=True)
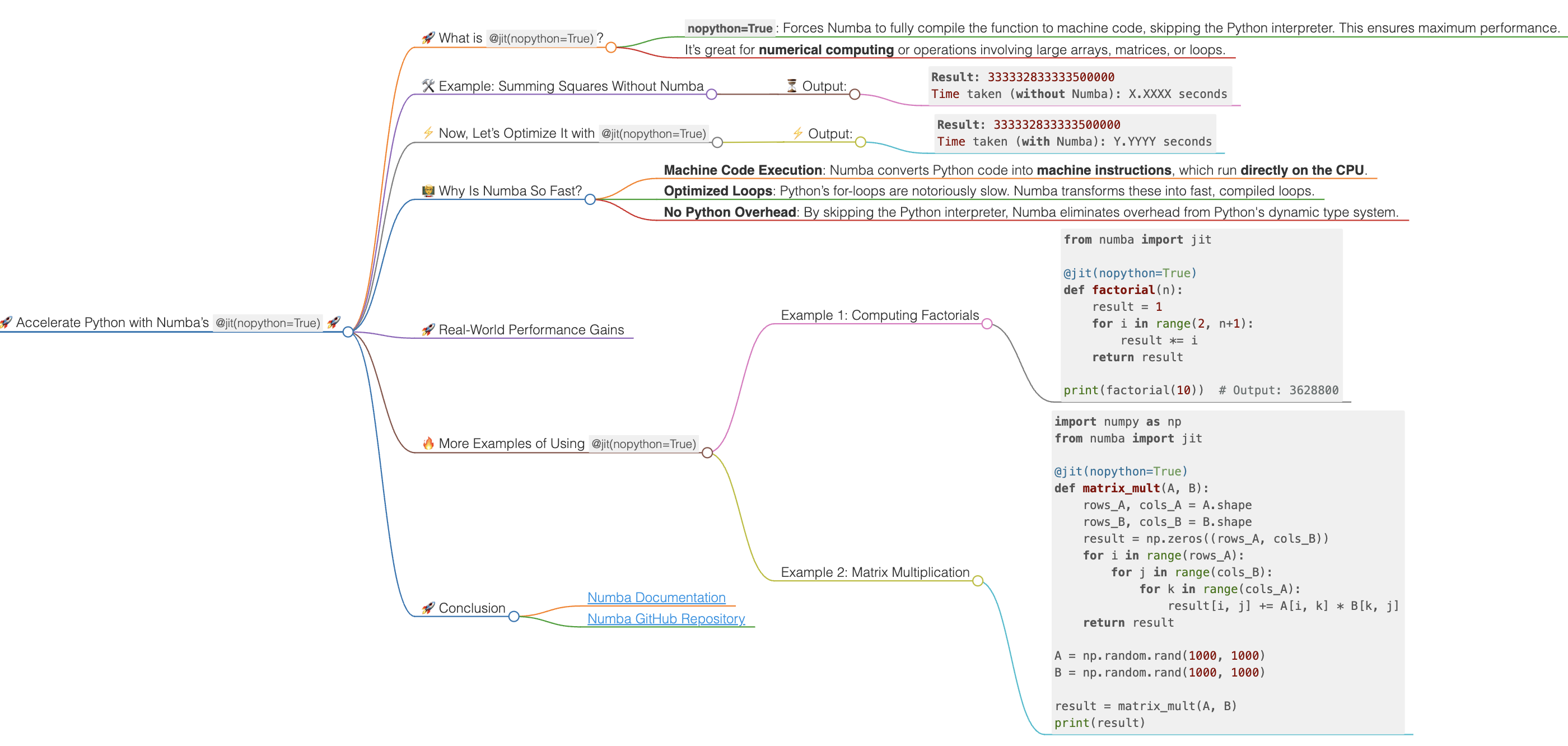
🚀 Accelerate Python with Numba’s @jit(nopython=True) 🚀
Are you looking to optimize your Python code for better performance? If you work with large datasets or run complex numerical computations, the Numba library can be a game-changer!
With @jit(nopython=True), Numba translates Python functions into machine code using Just-In-Time (JIT) compilation. This drastically reduces execution time, especially for loops and numerical operations.
Let me show you how it works! 👇
🚀 What is @jit(nopython=True)?
@jit(nopython=True) is a decorator from the Numba library. It compiles the entire function into machine code at runtime. Here’s why it’s special:
nopython=True: Forces Numba to fully compile the function to machine code, skipping the Python interpreter. This ensures maximum performance.- It’s great for numerical computing or operations involving large arrays, matrices, or loops.
💡 If Numba detects a dynamic type (like Python objects), it will throw an error with nopython=True, ensuring you stay in the compiled mode.
🛠️ Example: Summing Squares Without Numba
Let’s start with a simple Python function that computes the sum of squares of a list of numbers.
import time
# Regular Python function (without Numba)
def sum_of_squares(arr):
total = 0
for num in arr:
total += num * num
return total
arr = list(range(10000000)) # A list of 10 million numbers
start_time = time.time()
result = sum_of_squares(arr)
end_time = time.time()
print(f"Result: {result}")
print(f"Time taken (without Numba): {end_time - start_time:.4f} seconds")
⏳ Output:
Result: 333332833333500000
Time taken (without Numba): X.XXXX seconds
⚡ Now, Let’s Optimize It with @jit(nopython=True)
Here’s the same function, but this time we’ll add Numba’s @jit(nopython=True) to speed it up.
import time
from numba import jit
# Numba-optimized function using @jit(nopython=True)
@jit(nopython=True)
def sum_of_squares_jit(arr):
total = 0
for num in arr:
total += num * num
return total
arr = list(range(10000000)) # A list of 10 million numbers
start_time = time.time()
result = sum_of_squares_jit(arr)
end_time = time.time()
print(f"Result: {result}")
print(f"Time taken (with Numba): {end_time - start_time:.4f} seconds")
⚡ Output:
Result: 333332833333500000
Time taken (with Numba): Y.YYYY seconds
🧑🏫 Why Is Numba So Fast?
- Machine Code Execution: Numba converts Python code into machine instructions, which run directly on the CPU.
- Optimized Loops: Python’s for-loops are notoriously slow. Numba transforms these into fast, compiled loops.
- No Python Overhead: By skipping the Python interpreter, Numba eliminates overhead from Python’s dynamic type system.
🚀 Real-World Performance Gains
In this example, for 10 million numbers, the Numba-optimized function can run several times faster compared to the pure Python version. With even larger datasets or more complex computations, the performance gains will be even more impressive!
🔥 More Examples of Using @jit(nopython=True)
Example 1: Computing Factorials
from numba import jit
@jit(nopython=True)
def factorial(n):
result = 1
for i in range(2, n+1):
result *= i
return result
print(factorial(10)) # Output: 3628800
Example 2: Matrix Multiplication
import numpy as np
from numba import jit
@jit(nopython=True)
def matrix_mult(A, B):
rows_A, cols_A = A.shape
rows_B, cols_B = B.shape
result = np.zeros((rows_A, cols_B))
for i in range(rows_A):
for j in range(cols_B):
for k in range(cols_A):
result[i, j] += A[i, k] * B[k, j]
return result
A = np.random.rand(1000, 1000)
B = np.random.rand(1000, 1000)
result = matrix_mult(A, B)
print(result)
🚀 Conclusion
Numba is a powerful tool to boost the performance of your Python code, especially when dealing with numerical computations and large datasets. Using @jit(nopython=True), you can transform your slow Python functions into blazing-fast machine code with minimal effort.
Next time you need to optimize your Python code, give Numba a try!
🔗 Resources:
Feel free to connect with me for more tips on optimizing your Python code! 👨💻
#Python #Numba #MachineLearning #PerformanceOptimization #BigData #DataScience